カテゴリー: 数学と理科

バビロニアのゼロ

数の表し方

　「数」としてのゼロが使われる以前、「数」の表記において、ある位（くらい）に何もないとき、何もないことを表す記号が使われていました。

　例えば左から千円札1枚、百円玉2枚、1円玉3枚置いたとします。すぐに「1203円」であることがわかりますが、書いて表す（表記）するとしたら、順番通り123円ではおかしいです。やはり10円玉は1枚もありませんと宣言したほうがわかりやすいですね。ですから12Δ3円というふうに表すために「Δ」のような記号が使われていました。

　ところが、古代エジプトやギリシア、ローマでは10進法という10を底(てい)(10をひとまとめ)にする数え方を使った表し方～最先端～ではあったものの、ゼロを用いることがなかったので次のように表しました。
　ローマ数字　I(1)、V(5)、X(10)、L(50)、C(100)、D(500)、M(1,000)を用いると
　1203はMCCⅢ　となります。
　98だとLXXXXVⅢ　というように長くなります。

　ではこの2000年ほど前の時代「12Δ3」という最も進んだ記数法を使っていたのはどの地域でしょう？

バビロニアにゼロが登場

　バビロニアの数は60進法という60をひとまとまりに考えるものでした。

　1~59までは次のように表記します。社会で学習した楔形(くさびがた)文字です。

　バビロニアの数字　１～５９　Wikipediaから

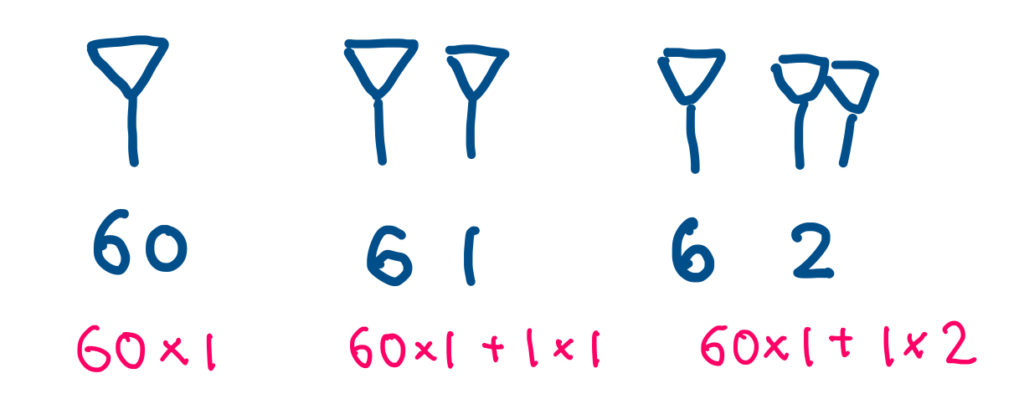
60と1が同じ表記になっています。これは「60が１つ」を表しているので、見た目は１と同じになります。次の61を見るとわかりやすいですね。「60×1＋1×1」＝「61」ということです。少し隙間が空いていて、左側は2桁目（60のまとまりがいくつあるか）、右側は1桁目（1のまとまりがいくつあるか）を表しています。
　このように一番右の位は1がいくつあるか、その左の位は60がいくつあるか、さらにその左の位は60²＝60×60＝3600がいくつあるか…を表しているのです。
　次は６９、７０、７１です。

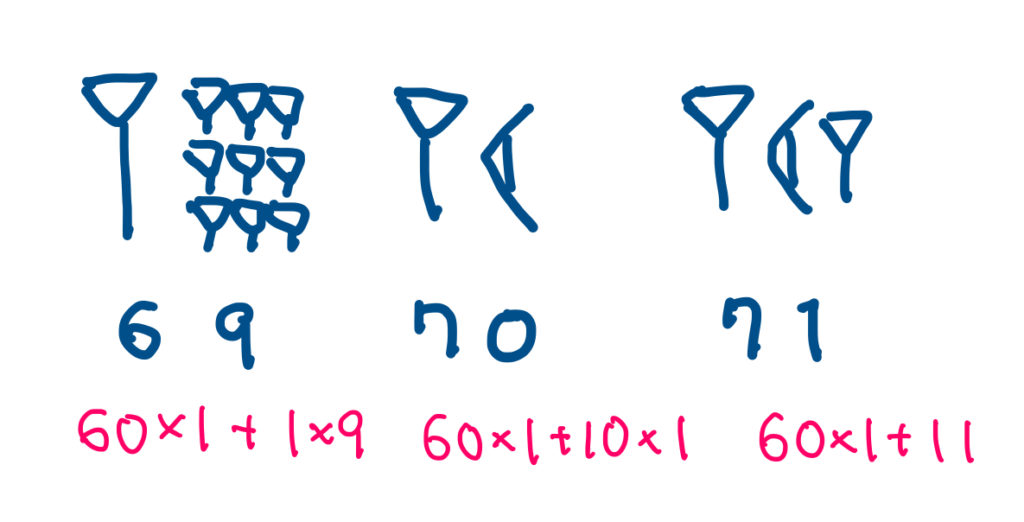
　紀元前300年ころまでは3601は61と同じ表記方法でした。つまり「60²×1＋60×０＋1×1」＝「3601」だったのです。これでは「61」の表記と区別がつかなくなります。そこで2桁目には何もないという意味で新しい記号を加えました。これが「ゼロ」です。（図の楔(くさび)が斜めに2つ並んだ部分）

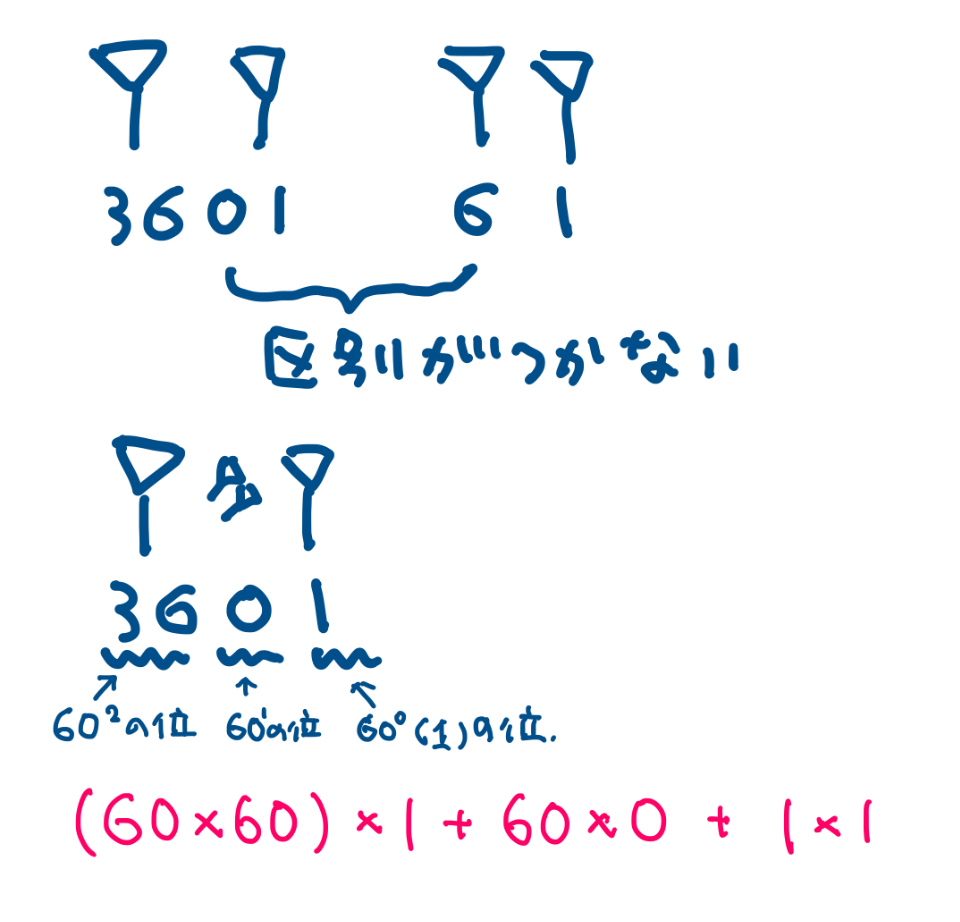
　見分けのつかない数字もあるのですが、それは文脈などでおぎなっていたそうです。

　＊右端の位には0記号は使えなかったので、2と120と7200はみな同じ表記になります。

　メキシコのマヤ文明にもバビロニアと同じような使い方のゼロがり、しかもマヤ文明では数の始まりがゼロでした。ただ、マヤとバビロニアの違いはマヤが20進法を使っていたという点です。

　紀元前4世紀にこのゼロがインドへ伝わります。数世紀の間アリストテレスやキリスト教の哲学の影響を受けなかったインドで「数」としてのゼロが生まれます。

☚ 算数いろいろ　ゼロについて④
　　算数いろいろ　エジプト式分数 ☛

紀元0年がなかったわけ

～無と無限は嫌われていた～

　紀元前4世紀　有名なギリシャ哲学者アリストテレスは「無」や「無限」を否定することで『神の存在』を証明しました。

　「宇宙は有限で地球はその中心にあり、外側の球を回しているものこそが神である。」という宇宙観です。

　また、アリストテレスは「自然は真空を嫌う」と言っています。

　この考えは中世ヨーロッパに継承され、宗教の一部となり、「無」について語ることは神の存在に疑問を投げかけることに等しいとされました。

　ですから、しばらくの間ヨーロッパにはゼロを使わない時代が続いたわけです。前回　紀元ゼロ年のお話で登場した修道士二人が紀元０年を作らなかったのはこのような背景のためです。

　みなさんは小学校でゼロという数を学習しますから、つい最近までゼロという数が存在しなかったことは信じられないのではないでしょうか。

　「ゼロ」が全く使われていなかったのかというと実はそうではありません。古代バビロニアや、メキシコのマヤ文明では「ゼロ」が使われていました。ただし、計算などで利用する「ゼロ」ではなく、数を表す「記数法」に「ゼロ」を利用していました。

　バビロニアの数は60進法という60をひとまとまりに考えるものでした。1~59までは次のように表記します。社会で学習した楔形（くざびがた）文字です。 次の機会に「ゼロ」の利用をお話しします。

☚ 算数いろいろ　ゼロについて③
　　算数いろいろ　ゼロについて⑤ ☛

紀元0年

　前々回「紀元も元号も０年は存在しません。」と書きました。再度そのお話です。

紀元0年がないのはなぜか

　6世紀　ローマ教皇から「むこう数百年分の復活祭の日付表を作成せよ」と依頼を受けた修道士ディオニシウス・エクシグウス。

　彼は、キリストが生まれた年を最初の年にすべきと考え、現在使われることとなった西暦の1年と決めました。(実際はキリストが生まれたと考えていた年の翌年の1月1日を暦の初めの日としました。)　

　＊しかしながら、現在キリストが生まれたのは紀元前4年と考えられていいます。

　こののち、次の復活祭日付表を作成した修道士ビードは「イギリス国民教会史」の最初の年を紀元前60年から始めたのですが、この暦には0年がありませんでした。この頃(中世)のヨーロッパではゼロを使用することがなかったからなのですが、これは問題ですよね。

ゼロ年がなかったことが何故問題なのか。

　たとえば、紀元前4年に生まれたキリストが生きていれば、今年紀元2020年には何歳になっていると思いますか？
　2020-(-4)＝2024歳と考えるのが普通ですが、実は2023歳なのです。紀元前3年に1歳、紀元前2年に2歳、紀元前1年に3歳　ここまではいいのですが、紀元1年に4歳となります。先ほどのように計算すると1-(-4)＝5歳となるはずですが、紀元0年がないために間違いが生じるのです。

　現在は21世紀です。世紀という単位は100年を1単位としていますから1世紀は紀元1年から紀元100年まで、2世紀は紀元101年から紀元200年まで・・21世紀は紀元2001年から2100年までとなっています。22世紀は2101年1月1日からです。

　私は世界史のテストの前に「０世紀があれば、よかったのにな」と思っていました。

　これでは天文学的事象の期間計算で不具合が生じます。

　天文学では紀元前1年を0年とし紀元前2年を-1年としています。ケプラーから始まり、単に紀元前1年を0年とするようになったのはカッシーニからです。

　横道にそれますが、土星探査機カッシーニの名前の由来になった天文学者です。2017年9月に探査機カッシーニは土星大気圏に突入して消えました。カッシーニから分離し土星の衛星タイタンに着陸したホイヘンスは今もタイタンにいるはずです。地球から最も遠い距離の天体にある人工物です。

　なぜ中世のヨーロッパではゼロを使わなかったのでしょう？

☚ 算数いろいろ　ゼロについて②
　　算数いろいろ　ゼロについて④ ☛

　「ゼロについて①」で「紀元も元号も０年は存在しません。」「天文学では紀元前１年を0年とし、紀元前２年を－1年としています。」と基点を表すゼロについて書きましたが、今回は起算日のゼロについてです。

　ある出来事の期間が満了するときは、起算日の前日が満了日(定められた期限が来て期間が終わる日のこと)となります。注　ここから少し話がややこしくなります。

　起算日は初日を除く翌日とするので、期間が終わる(満了する)日はある出来事が起きた日の翌日（起算日）の前日だから、ある出来事が起きた日となります。

　ところが、年齢計算の場合、例外的に誕生日を起算日としているので、満了するのが起算日（誕生日）の前日ということになります。

　日本の法律では、誕生日の前日の午後12時に満了し１つ年をとることになるので、毎年やってくる誕生日は法律上は「1つ歳をとった日の翌日」ということになります。

　4月1日生まれの人はその年の1月～3月に生まれた人と同じ学年になり、4月2日に生まれた人は次の学年になるわけです。

　2月29日生まれの人は法律上は毎年2月28日午後12時に１つ年をとることになります。

　さらに、年齢には「数え年」という数え方があります。

　数え年は、生まれた時の最初の年を１年とし以降１月１日が来るごとに１歳ずつ加える数え方です。

　数え年では12月31日に生まれたらその時が１歳で翌日元旦を迎えると２歳になります。

　「数え年」では０歳がありません。

　韓国では数え年で年齢を数えるそうです。

　妊娠した時も「妊娠０カ月」はありません。 競走馬は生まれた時０歳で元旦を迎えるごとに１歳加えていきます。

☚ 算数いろいろ　ゼロについて①
　　算数いろいろ　ゼロについて③ ☛

ゼロでわること～ゼロでわってはいけない理由～

　2012年に、ある小学校の授業中のテストで出題された　『９÷０』　という計算問題が話題になりました。

　問題を出した先生の生徒への解答が　『９÷０＝０』　だったということで、間違いを指摘するツイートが拡散したようです。

　本当の答えは　『９÷０は計算できない』（『０で０以外の数字をわってはいけない』）です。

　何故計算できないのでしょう。

　ゼロという数字について少し考えてみました。

１　ゼロでわってはいけない理由

　9÷0＝a　だとします。

　両辺に0をかけると

　9÷0×0＝a×0　となります。

　9を0で割って0をかけているので、左辺は9です。

　どんな数も0をかけると0なので、右辺は0です。

　ということは　9＝0　となってしまいます。

　「ゼロでわってはいけない。」というより、ゼロでわっても答えは出ない、ゼロでわることは不可能ということです。

　ゼロでわるとどうなるか。そのことは、次回にお話します。

２　いろいろなゼロ

　①基点を表すゼロ

　紀元も元号も０年は存在しません。紀元１年（元年）の前の年は紀元前１年となります。

　ただ、インドのヒンドゥー暦は西暦78年をインド国定暦0年としているそうです。

　天文学では紀元前１年を0年とし、紀元前２年を－1年としています。

　②年齢のゼロ

　満年齢の数え方は、誕生した日や年を「０歳」「０年」とします。

　妊娠した時も「妊娠０カ月」はありません。(お母さんかお父さんに聞いてみてください)

　競走馬は生まれた時０歳で元旦を迎えるごとに１歳加えていきます。

　③いろいろなゼロ

　電気抵抗が０になると超伝導といいます。

　日本では　皇紀２６００年（西暦１９４０年）に採用された兵器につけた型式が　陸軍では100式　海軍では零式でした。

　テニスでは０点を「ラブ」といいます。フランス語の「たまご」です。

☚ 算数いろいろ　素数②
　　算数いろいろ　ゼロについて② ☛

＜未解決問題＞

　古今東西最大の数学者であるガウス（1777～1855）は、かつてこう言いました。「数学は科学の女王であり，整数論は数学の女王である」

　数学の一分野である「整数論」には，問題の意味は小学生にも理解できるけれど，いまだ誰にも解決されていないといったタイプの未解決問題がたくさんあり，最近証明されて話題になった「フェルマーの定理」などもその１つでした。素数に関係する有名な未解決問題には，「双子素数の問題」や，「ゴールドバッハの予想」などがあります。

　素数なんてつまらないかもしれませんが、実は生活に密接に関係しています。

　「ベリサイン」というインターネット通信関連の会社の金庫に大切に保管されているのが膨大な素数表です。この素数表にある大きな素数を使ってカードの暗証番号などを暗号化しているのです。(大きな数の因数分解は大変難しく、大きな素数を必要とします。)素数を使うことで公開鍵暗号方式（RSA）という暗号化の仕組みが開発されました。素数は現代の生活になくてはならないアイテム(道具)となっています。

　ところで、数学者が素数の仕組みを証明してしまうと、この暗号方式では危険なのではないかと心配する人もいると思います。が、暗号を解くことはできるようになっても膨大な時間がかかります。ですから、素数の仕組みが分かってもこの暗号方式は、かなり安全だと考えられます。

　ちなみに、アメリカの国防総省では、「リーマン予想(素数についての予想　いまだ未解決)を証明した」という論文が発表されると、本当に証明できているかどうかチェックする部署があるそうです。でもそのチェックにも数年かかります。

＜双子素数の問題＞

　素数には，（３，５），（１１，１３）のように，１つおきに並ぶペアになっているものがあって，これらを「双子素数」といいます。（ちなみに、３と７のように差が４である素数の組を「いとこ素数」　、5と11のように差が６である素数の組をセクシー(sixから？)素数　といいます）

　１００以下の双子素数は以下の７ペアです。

　(３，５) （５，７） （１１，１３） （１７，１９） （２９，３１） （４１，４３） （７１，７３）　

　このような「双子素数」は『無限に多く存在する』らしいのですが、いまだに証明されていません。なお，2020年5月の時点で知られている最大の双子素数は388,342桁の2996863034895× 2^1290000 ± 1です。

＜ゴールドバッハの予想＞

　４＝２＋２，６＝３＋３，８＝３＋５，１０＝３＋７，１２＝５＋７・・・のように，「４以上のすべての偶数は２つの素数の和で表される」という予想です。これもほとんどの数学者が正しいと信じていますが，いまだ未証明。

　中学1,3年生や高校1年生が現在学習中の「素数」についての話です。

＜素数とは？＞

　ふつう，数は，自分自身よりも小さな数のかけ算の形にいろいろと表すことができます。

　例えば，３６という数は・・・・・

　３６＝６×６ ３６＝１２×３ ３６＝１８×２　などのように，いろいろと形を変えることができます。しかし，これらをさらに細かく，

　３６＝６×６＝（２×３）×（２×３）

　３６＝１２×３＝（２×２×３）×３

　３６＝１８×２＝（２×３×３）×２　のように，これ以上分解できなくなるまで細かく分けていくと，最後にはすべて，３６＝２×２×３×３　という形になります（１はいくつかけても変わらないので，この場合考えません）。

　このように，すべての数は，これ以上分解できないかけ算の形に１通りに表すことができ，このとき現れる「これ以上分解できない数」のことを「素数」，数を素数に分解することを「素因数分解する」といいます。

　素数とは，１と自分自身以外には約数をもたない数のことです（１は素数に数えません）。すべての物質が原子という基本元素からなるように，すべての数は素数という数の元素から構成されているのです。

＜素数はどれくらいあるか？＞

　自然界の構成要素である原子の個数は高々１００いくつ(現在予測されているのは173番まで)ですが，素数はどれくらいあるのでしょうか。

　結論から先にいうと，素数は自然数と同じように，無限にあるのです。「１と自分自身以外に約数がない」という，ある意味とても限定された条件をみたす数が無限にあるというのは，ちょっと信じがたい気もします。しかし，これは今から２３００年も昔のギリシャ時代，すでにユークリッドが「原論」という本の中で見事に証明しています。けっして難しい証明ではないので下にのせました。興味のある方はご覧になってください。（特に高校1年生）

＜素数が無限にあることの証明＞　背理法(高校1年で学習)

　素数が有限個しかないと仮定する。

　最大の素数をＰとして，Ｑ＝１×２×３×４×･･･×Ｐ＋１という数を考える。

　Ｑを素数とすると・・・・・・Ｐが最大の素数であるということに矛盾。

　Ｑが素数でないとすると・・・・・・ＱはＰ以下のいずれかの素数で割り切れるはずだが，Ｑの形より，Ｑは２からＰまでのすべての数で割り切れないので矛盾。

　いずれにせよ，矛盾。

　これにより，素数が有限個であるという最初の仮定があやまりであることがわかる。 よって，素数は無限にある（証明終了）

☚　算数いろいろ
　　算数いろいろ　素数②　☛

　小中高校生に向けた数学についてのお話です。

　いろいろな数字のことを調べてみました。

　バビロニアの楔形文字や、０(ゼロ)のこと、日本の数字や計算のことなどです。

　算数いろいろ　素数①　☛